并查集就是一个数组 father[] ，father[i] 表示元素 i 的父节点。

并查集的使用场景主要有：

• 寻找节点的公共根结点
• 判断图的连通性
• 求集合的个数（根据给定的数据，求这些数据能够构成几个不连通的图）
• …

并查集的几个操作：

初始化

for (int i = 0; i < N; i++) {
    father[i] = i;
}

查找

用于快速找到某个节点的根结点

function findFather(x) {
    while (father[x] !== x) {
        x = father[x];
    }
    
    return x;
}

// or 递归
function father(x) {
    if (x === father[x]) {
        return x;
    }
    return findFather(father[x]);
}

合并

function union(a, b) {
    let fa = findFather(a);
    let fb = findFather(b);
    if (fa !== fb) {
        father[fa] = fb; // 将 a 接在 b 之下，即 b 作为 a 的父节点
    } // 否则，出现了环
}

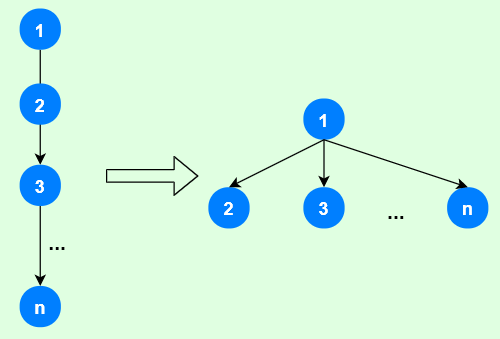
路径压缩

若节点很多的情况下，并查集的"高度"会非常高，因此可以使用路径压缩，使所有结点与根节点直接相连。

function findFather(x) {
    let tmp = x;
    while (x !== father[x]) { // 寻找根结点，根结点是父节点等于当前值的节点
        x = father[x];
    }
    
    while (tmp !== father[tmp]) {
        let a = tmp;
        tmp = father[tmp];
        father[a] = x; // 将原先节点的父节点直接改为根结点。
    }
    
    return x; // 返回根结点
}

// 递归写法
function findFather(x) {
    if (x === father[x]) {
        return x;
    }
    
    let r = findFather(father[x]);
    father[x] = r;
    return r;
}