https://leetcode-cn.com/problems/redundant-connection-ii/

难度：困难

---

  在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。每一个节点只有一个父节点，除了根节点没有父节点。

  输入一个有向图，该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。

  结果图是一个以边组成的二维数组。 每一个边 的元素是一对 [u, v]，用以表示有向图中连接顶点 u 和顶点 v 的边，其中 u 是 v 的一个父节点。

  返回一条能删除的边，使得剩下的图是有N个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

简化题目： 根据给定的边集，求出一条多余的边，使得删除这条边后，图会变成一棵树，对于一些情况，这样的边会有多条，删除边集中出现的最后一条满足条件的边。

示例 1:

输入: [[1,2], [1,3], [2,3]]

输出: [2,3]

解释: 给定的有向图如下:

  1
 / \
v   v
2-->3

示例 2:

输入: [[1,2], [2,3], [3,4], [4,1], [1,5]]

输出: [4,1]

解释: 给定的有向图如下:

5 <- 1 -> 2
     ^    |
     |    v
     4 <- 3

注意:

• 二维数组大小的在3到1000范围内。
• 二维数组中的每个整数在1到N之间，其中 N 是二维数组的大小。

解法1：并查集

思路来源：Nu11Pointer

  对于一条能使一棵树变成图的边，它有以下几种情况：

1. 

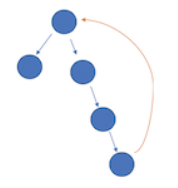
   这条边从任意节点出发，指向了根结点，此时树形成了环，树也就没有根结点了（表现就是所有结点的入度都为 1），而这种情况下，处于这个环中的所有边都能被删除，因为删除任意一条边都能变成一棵正常的树，这也就是题目中提到的“多条边”的情况，但根据题目，需要删除边集中最后一条在环中的边。

2. 

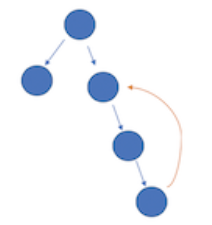
   这条边从任意节点出发，指向了其祖先节点，树中形成了环，但仍有根结点，不过造成的后果就是有一个节点的入度变成 2了。这种情况下，只能删除环中的且造成 2 个入度的边，即图中橙色的边。

3. 

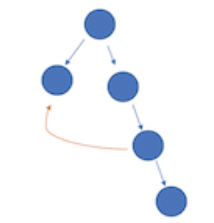
   这条边从任意节点出发，指向了一个非祖先节点。这种情况下，有一个节点的入度会为 2，这两条造成入度为 2 的边都能删除，但根据题目，需要删除后出现的那条。

  

  好了，既然清楚可能的几种情况，就需要想办法找到这些满足条件的边了。

  对于这种需要判断环的问题，可以考虑使用并查集来做。在创建并查集的过程中，合并两个节点 a 和 b 时，若这两个节点有着公共的根结点，那么将它们合并的话就会出现环了。

  好的，首先，我们可以判断图中是否存在入度为 2 的节点，若存在，那么就是第 2 和第 3 种情况，将造成入度为 2 的这两条边（edge1，edge2）都先记录下来。

  然后创建并查集，我们跳过 edge2 （后出现的边）这条边，若创建并查集的过程一路畅通（即未出现环），那么答案就是 edge2，也就是 2. 中删了正确的边（橙色的边）和 3. 中的情况 。

  而若创建并查集的过程中出现了环，那么对应的就是 2. 中删除了错误的边，那么答案就是 edge1。

  若不存在入度为 2 的节点 ，那么就是 1. 中的情况了。此时，在创建并查集的过程中，记录那条造成环出现的边，这条边会是环中的边（废话），且会是边集中最后出现的满足条件的边，将其记录下来，作为答案返回。

JS 代码：

var findRedundantDirectedConnection = function(edges) {
    let inDegrees = [];
    let res = [];
    let meetCircle;

    for (let edge of edges) {
        let node = edge[1];
        if (!inDegrees[node]) {
            inDegrees[node] = edge;
        } else {
            res.push(inDegrees[node]);
            res.push(edge); // 若找到入度为 2 的节点，将其中一条边记录下来
            break;
        }
    }

    let father = [];

    for (let i = 1; i <= edges.length; i++) {
        father[i] = i;
    }

    const findFather = (x) => {
        let tmp = x;
        while (x !== father[x]) {
            x = father[x];
        }

        let a = tmp;
        tmp = father[tmp];
        father[a] = x;

        return x;
    };

    const union = (a, b) => {
        let fa = findFather(a);
        let fb = findFather(b);
        if (fa !== fb) {
            father[fb] = fa;
        } else { // 遇到了环
            meetCircle = [a, b];
        }
    };

    // 建立并查集，若存在入度为 2 的节点，跳过后出现的边
    for (let edge of edges) {
        if (res.length && res[1] === edge) {
            continue;
        }
        union(edge[0], edge[1]);
    }

    // 若没有入度为 2 的点，则说明冗余的边指向了根结点
    if (res.length === 0) {
        return meetCircle;
    }

    return meetCircle ? res[0] : res[1];
};

  优化后的代码：只遍历了一次边集

var findRedundantDirectedConnection = function(edges) {
    let res = [], father = [];
    let indegrees = [];
    let meetCircle;

    const findFather = (x) => {
        let tmp = x;
        while (x !== father[x]) {
            x = father[x];
        }

        let a = tmp;
        tmp = father[tmp];
        father[a] = x;

        return x;
    };

    // 创建并查集
    for (let edge of edges) {
        let node1 = edge[0], node2 = edge[1];

        // 初始化
        if (!father[node1]) {
            father[node1] = node1;
        }
        if (!father[node2]) {
            father[node2] = node2;
        }

        if (indegrees[node2]) { // 若其入度已经为 1 了，则加上当前边入度就是 2了
            res.push([indegrees[node2], node2]);
            res.push(edge);
        } else {
            indegrees[node2] = node1;
            let f1 = findFather(node1);
            let f2 = findFather(node2);
            if (f1 !== f2) {
                father[f2] = f1;
            } else { // 遇到了环
                meetCircle = edge;
            }
        }
    }
    
    // 若没有入度为 2 的点，则说明冗余的边指向了根结点
    if (res.length === 0) {
        return meetCircle;
    }

    // 否则，根据是否产生环输出答案
    return meetCircle ? res[0] : res[1];
};