要理解坐标系间的转换过程，需要提前了解：

1. ThreeJS 中的几种坐标系
2. 屏幕坐标系和标准设备坐标系

  不想看链接中的内容这边也有不规范的简述：

  物体的坐标转换过程大致为：局部坐标 -> 世界坐标 -> 观察空间坐标 -> 裁剪空间坐标 -> 屏幕空间坐标

  我们将 观察空间坐标系 和 裁剪空间坐标系 之间的转换统一处理，最终得到 标准设备坐标系

  因此坐标转换过程就变成了：局部坐标 -> 世界坐标 -> 标准设备坐标 -> 屏幕空间坐标

  原本世界坐标转换到观察空间坐标需要乘上视图矩阵 CameraMatrixWorldInverse(ViewMatrix)

  随后，观察空间坐标转换到裁剪空间坐标需要乘上相机投影矩阵：ProjectMatrix

  在 ThreeJS 中有一个方法 Vector3.project(camera) 综合了这两步：

project( camera ) {
    return this.applyMatrix4( camera.matrixWorldInverse ).applyMatrix4( camera.projectionMatrix );
}

屏幕坐标系和标准设备坐标

  ThreeJS 是使用了 canvas 画布绘制图形的，因此屏幕坐标系就是 canvas 中的坐标系，也就是左上角是坐标原点：

  在 ThreeJS 中，一个物体可看作一个 Mesh，Mesh 的坐标是用一个 Vector3 来表示的，Vector3 中包含了 x、y、z 坐标。

  空间坐标系是三维的，其原点默认在屏幕中心，且 x y z 的范围是 [-1,1]，因此其 x、y 轴在屏幕坐标系中的表示就是：

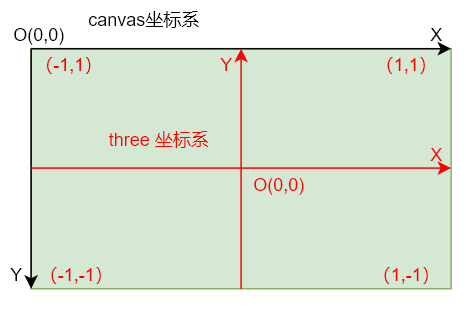
屏幕坐标转世界坐标

  屏幕坐标转空间坐标需要经过两个步骤：屏幕坐标 -> 标准设备坐标 -> 世界坐标

ThreeJS 中，画布一般是全屏的，因此画布的宽高 w,h 就是：window.innerWidth 和 window.innerHeight，所以 Three 的空间坐标系中点 (cx, cy)在屏幕坐标系中就是：(w / 2,h / 2)。

（根据情况，有时候宽高会是 canvas.offsetWidth 和 canvas.offsetHeight）

假设 canvas 中有一点 (x,y)，这个点在空间坐标系中为 (x1,y1)，那么这个转换公式是：

$x1 = (x / w) * 2 - 1$

$y1 = -(y / h) * 2 + 1$

公式推导过程如下：

1. 首先，我们知道了空间坐标系中点在屏幕坐标系中的表示：$cx = w / 2$，$cy = h / 2$

2. 那么，屏幕坐标系中的点 $(x, y)$ 应用这个原点 $(cx, cy)$ 后的表示为：$x' = x - cx$，$y' = cy - y$ （因为这两个坐标系的 y 轴方向是相反的）

3. 然后再将 $(x', y')$ 标准化到 $[-1, 1]$ 之间，也就是分别除以 $cx$ 、$cy$ ：

   $\frac{x'}{cx} = \frac{x - cx}{cx} = \frac{x}{\frac{w}{2}} - 1 = (x / w) * 2 - 1$

   同理：

   $\frac{y'}{cy} = \frac{cy - y}{cy} = 1 + \frac{-y}{\frac{w}{2}} = -(y / h) * 2 + 1$

使用代码表示就是：

const x = event.clientX;//鼠标单击坐标X
const y = event.clientY;//鼠标单击坐标Y

// 屏幕坐标转标准设备坐标
const x1 = ( x / window.innerWidth ) * 2 - 1;
const y1 = -( y / window.innerHeight ) * 2 + 1;
//标准设备坐标(z=0.5这个值并没有一个具体的说法)
const stdVector = new Vector3(x, y, 0.5);

然后，再通过 Vector3.unproject(camera) 方法将标准设备坐标转为世界坐标：

const worldVector = stdVector.unproject(camera);

世界坐标转屏幕坐标

与上面的坐标转换相反，世界坐标转屏幕坐标的过程为：世界> 标准设备坐标 -> 屏幕坐标

  通过 Vector3对象的方法 project(camera)，返回的结果是世界坐标 worldVector在 camera相机对象矩阵变化下对应的标准设备坐标， 标准设备坐标 xyz 的范围是[-1,1]。

同样的，假设画布宽为 w ，高为 h，屏幕坐标系中的一点为 (x, y)，标准设备坐标系中对应的点为 (x1, y1)

  从标准设备坐标系转换到屏幕坐标系与我们前面计算出的公式相反：

$x = x1 * \frac{w}{2} + \frac{w}{2}$

$y = y1 * \frac{h}{2} - \frac{h}{2}$

  首先计算出屏幕坐标系中心：

const centerX = window.innerWidth / 2;
const centerY = window.innerHeight / 2;

  计算出的 centerX 和 centerY 同时也表示了坐标轴的一半大小。

  然后，将设备坐标系使用 project 方法转换到标准设备坐标系，再转换到屏幕坐标系中：

const standardVec = worldVector.project(camera);

const screenX = Math.round(centerX * standardVec.x + centerX);
const screenY = Math.round(-centerY * standardVec.y + centerY);